【講義】連立方程式とグラフ
- 正解率:15.38%
- 解答数:13
EXAMPLE
例題
次の連立方程式をグラフを用いて解き,ア,イに当てはまる数を半角英数字で入力しなさい。また,計算でも解いて確かめなさい。
\[ \begin{cases}
3x -2y =4 &\cdots \cdots ① \\
2x +y =5 &\cdots \cdots ②
\end{cases} \]
\[ x =\fbox{ア}, \quad y =\fbox{イ} \]
TEXT
テキスト解説
方程式$ax +by =c$のグラフが次の図の①の直線,$px +qy =r$のグラフが次の図の②の直線であるとします。
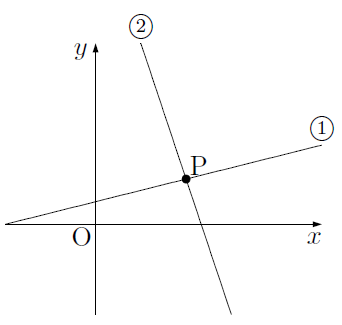
この直線上の点の座標は,それぞれの方程式の解になっているので,2つの直線の交点(上図の点P)は,2つの方程式の共通の解ということになります。つまり,点P(2直線の交点)の座標が,次の連立方程式の解になります。
\[ \begin{cases}
ax +by =c &\cdots \cdots ① \\
px +qy =r &\cdots \cdots ②
\end{cases} \]
ただし,2つの方程式のグラフが同じになるとき,共通な解は無数に存在(このような連立方程式は不定といいます)し,2つの方程式のグラフが平行になるときは,交点を持たないので共通な解は存在しない,つまり,連立方程式の解はありません(このような連立方程式は不能といいます)。
このようにして,方程式をグラフで表すことにより,方程式の解を視覚的に判断ができるようになります。さらに,図に表すことで,図形の性質を利用して解を求めることもできる場合もあります。方程式とグラフとの密接な関係をしっかりと理解し,それを利用できるようにしましょう。
MOVIE
動画解説
