【講義】直線の傾きと切片
- 正解率:100.00%
- 解答数:4
EXAMPLE
例題
次の直線の傾きと切片を求め,ア~オに当てはまる数を半角英数字で入力しなさい。ただし,$\displaystyle -\frac{1}{2}$のような分数は,$\displaystyle \frac{-1}{2}$のように分子に符号を含む形で入力すること。
- $y =2x -5$
\[ \text{直線の傾き:} \fbox{ア} \quad \text{直線の切片:} \fbox{イ} \] - $\displaystyle y =-\frac{2}{3}x +3$
\[ \text{直線の傾き:} \frac{\fbox{ウ}}{\fbox{エ}} \quad \text{直線の切片:} \fbox{オ} \]
TEXT
テキスト解説
直線が$x$軸に対してどれくらい傾いているかを数値にしたものを傾きといいます。この「直線がどれくらい傾いているのか」ということを,次のグラフのように,「$x$の増加量に対して,$y$がどれくらいの割合で増加するか」ということを考えることで,直線の傾きを数値で表すことができます。
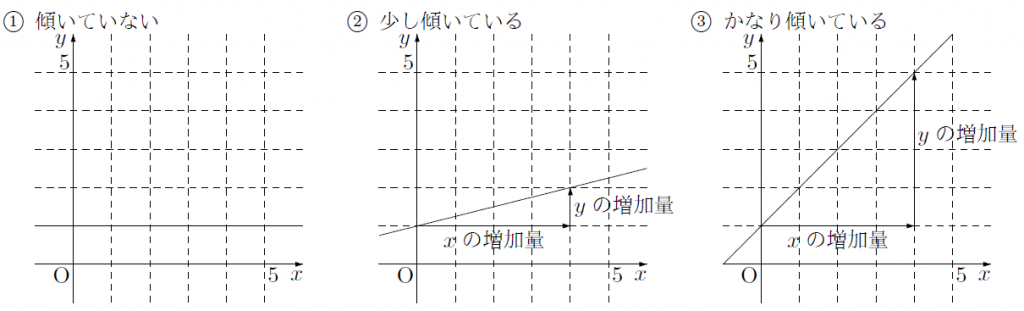
つまり,直線の傾きを,
\[ \text{(傾き)} =\frac{y\text{の増加量}}{x\text{の増加量}} \]
という式で表せることになりますが,この式は「変化の割合」と同じ式です。このことから,1次関数$y =ax +b$では,
\[ \text{(変化の割合)} =\text{(傾き)} =\frac{y\text{の増加量}}{x\text{の増加量}} =a \]
という関係が成り立ちます。
また,直線と$y$軸との交点の$y$座標のことを$y$切片(切片)といいます。1次関数$y =ax +b$のグラフは次のように,点$(0, \ b)$を通る直線であったので,1次関数$y =ax +b$のグラフは,「傾き$a$,切片$b$の直線」のように言い表すことがあります。
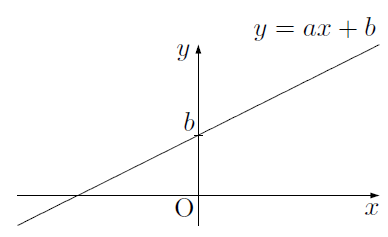
MOVIE
動画解説
