【講義】座標平面上の最短距離
- 正解率:25.77%
- 解答数:392
EXAMPLE
例題
次の図のように,2点A$(4, \ 3)$,B$(0, \ 2)$があります。$x$軸上に点Pを$\text{AP} +\text{PB}$の長さが最短になるようにとるとき,点Pの座標を求め,ア~ウに当てはまる数を半角英数字で入力しなさい。
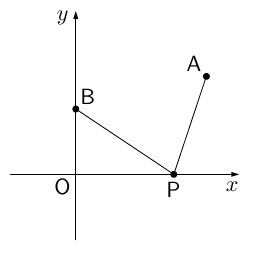
\[ \text{P} \ \left( \frac{\fbox{ア}}{\fbox{イ}}, \ \fbox{ウ} \right) \]
TEXT
テキスト解説
次の図のように,座標平面上に2点A,Bがあります。
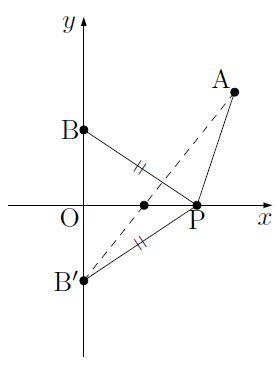
また,$x$軸上に点Pをとりますが,$\text{AP} +\text{PB}$の長さが最短となるようにするにはどうすればよいのかを考えます。
まず,点Bと$x$軸について対称な点B’をとります。すると,$\text{PB} = \text{PB’}$になるので,
\[ \text{AP} + \text{PB} =\text{AP} + \text{PB’} \]
このことから,$\text{AP} +\text{PB}$の長さが最短になるには,$\text{AP} + \text{PB’}$の長さが最短となるように点Pをとればよく,そのとき,A,B’,Pは一直線(上図の点線)上に並ぶことになります。
このように,複数の点を結ぶ線分の長さが最短となるためには,それらの点が一直線上に並ばなければいけませんが,結んだ線分の中継点(点P)に対して端の点(点A,B)が同じ側にある場合,一直線に点を並べることができません。そこで,結んだ線分の端の点(点A,B)と中継点(点P)を通る線を軸($x$軸など)について対称な点をとることで,一直線に点を並べることができるようになります。
MOVIE
動画解説
