【講義】傾きと座標(公式)
- 正解率:100.00%
- 解答数:1
EXAMPLE
例題
次の条件をみたす1次関数の式を求め,ア~オに当てはまる数を半角英数字で入力しなさい。ただし,$\displaystyle -\frac{1}{2}$のような分数は,$\displaystyle \frac{-1}{2}$のように分子に符号を含む形で入力すること。
- 点$(1, \ 2)$を通り,傾き$-3$の直線。
\[ \textbf{1次関数の式:} y =\fbox{ア}x +\fbox{イ} \] - $x =-6$のとき$y =5$であり,$x$の値が3ずつ増加すると$y$の値は2ずつ減少する直線。
\[ \textbf{1次関数の式:} y =\frac{\fbox{ウ}}{\fbox{エ}}x +\fbox{オ} \]
TEXT
テキスト解説
次の図のような,点$(p, \ q)$を通り傾き$a$の直線について考えます。
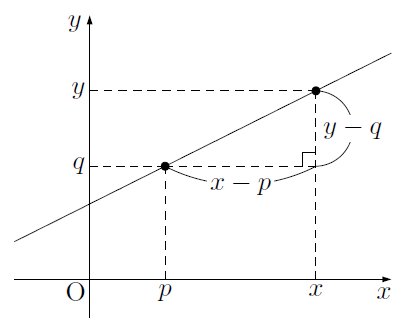
このとき,点$(p, \ q)$と異なる直線上の任意の点を$(x, \ y)$とすると,直線の傾きが$a$であることから,
\[ \text{(直線の傾き)} = a =\frac{y\text{の増加量}}{x\text{の増加量}} =\frac{y -q}{x -p} \]
という関係が成り立つので,
\begin{align}
\frac{y -q}{x -p} &=a \\
y -q &=a(x -p) \\
y &=a(x -p) +q
\end{align}
という公式を導くことができます。
MOVIE
動画解説
