【講義】1次関数のグラフ
EXAMPLE
例題
1次関数
- $\displaystyle y =\frac{1}{2}x$
- $\displaystyle y =\frac{1}{2}x +3$
- $\displaystyle y =\frac{1}{2}x -2$
について以下の問いに答えなさい。
(i) 下のような$x$と$y$の対応表を完成させなさい。

(ii) (i)の表から,それらに対応する点$(x, \ y)$を図にかき入れ,その点をなめらかに結ぶことにより,1次関数のグラフをかきなさい。
TEXT
テキスト解説
1次関数$y =ax +b$は,$y =ax$の式から,
\[ y =ax \longrightarrow y =ax +b \]
となることによって,$x$に対応する$y$の値が$b$だけ増えることがわかります。

このことから,1次関数$y =ax +b$のグラフは,$y =ax$のグラフを,「$y$軸の正の方向に$b$だけ平行移動したグラフ」だと考えることができます。
$y =ax$のグラフ(比例のグラフ)は,原点を通る直線でした。原点$(0, \ 0)$を$y$軸の正の方向に$b$だけ移動させると,
\[ (0, \ 0) \longrightarrow (0, \ b) \]
となるので,1次関数$y =ax +b$のグラフは「$y =ax$に平行で,$(0, \ b)$を通る直線」だということができます。
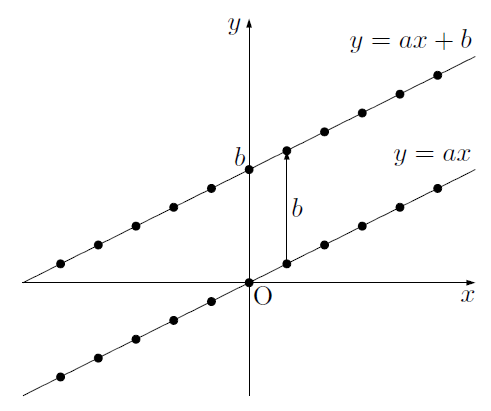
このように,1次関数$y =ax +b$のグラフは直線になり,この直線を「直線$y =ax +b$」といい,$y =ax +b$を直線の式といいます。
MOVIE
動画解説
