【講義】一直線上にある3点
- 正解率:18.48%
- 解答数:184
EXAMPLE
例題
3点$(-5, \ -9)$,$(p, \ 3)$,$(5, \ 11)$が一直線上にあるとき,$p$の値を求め,アに当てはまる数を半角英数字で入力しなさい。
\[ p =\fbox{ア} \]
TEXT
テキスト解説
2点が決まると,その2点を通る直線を1本だけかくことができます。つまり,2点が決まると直線はただ1つに決まります。
次の図のように,2点A,Bがあるとき,その2点A,Bを通る直線はただ1つだけ存在します。そのため,2点A,B,Pが一直線上にあるためには,2点A,Bを通る直線上に点Pがあればよいことになります。
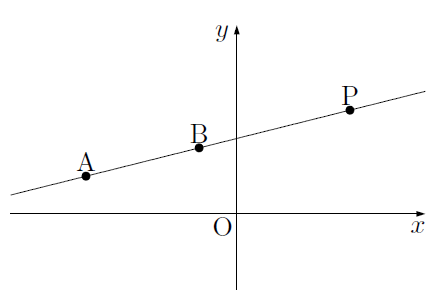
また,直線の傾きと通る1点がわかるとき,直線の式を求めることができました。つまり,直線の傾きと通る1点が同じであれば,同じ直線の式になり,そのグラフも同じになります。直線ABとAPは点Aが同じであるので,2つの直線の傾きが等しければ同じ直線になります。2つの直線が同じであれば,2点A,B,Pは一直線上に並んでいることになります。
このことから,3点が1直線上にある場合,次のいずれかの条件が成り立てばよいことになります。
- 2点を通る直線上にもう1点もある
- 異なる2点を通る2つの直線(AB,AP,BP)が同じ直線になる
MOVIE
動画解説
