【講義】対称な点の座標
- 正解率:25.00%
- 解答数:64
EXAMPLE
例題
点A\( (3, \ 4) \)について次の座標を求め,ア~カに当てはまる数を半角英数字で入力しなさい。
- \( x \)軸に関して対称な点B\( \left( \fbox{ア}, \ \fbox{イ} \right) \)
- \( y \)軸に関して対称な点C\( \left( \fbox{ウ}, \ \fbox{エ} \right) \)
- 原点に関して対称な点D\( \left( \fbox{オ}, \ \fbox{カ} \right) \)
TEXT
テキスト解説
次の図のような点A\( (a, \ b) \)について,\( x \)軸に関して対称な点(\( x \)軸を基準に折り曲げるとちょうど点Aと重なる点)をBとします。
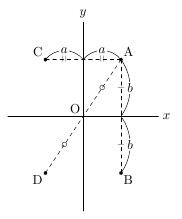
このとき,点Aから\( x \)軸までの距離と点Bから\( x \)軸までの距離は等しくなるので,点Bの座標は,
\[ \textbf{B}(a, \ -b) \]
と表すことができ,\( x \)座標は変わらず,\( y \)座標の符号が変わります。
また,点Aについて\( y \)軸に関して対称な点(\( y \)軸を基準に折り曲げるとちょうど点Aと重なる点)をCとします。このとき,点Aから\( y \)軸までの距離と点Cから\( y \)軸までの距離は等しくなるので,点Cの座標は,
\[ \textbf{C}(-a, \ b) \]
と表すことができ,\( y \)座標は変わらず,\( x \)座標の符号が変わります。
次に,点Aについて原点に関して対称な点(点Oを基準に点Aの反対側にある点)をDとします。このとき,点Aから原点までの距離と点Dから原点までの距離は等しくなり,点Dは,点Bについて\( y \)軸に関して対称な点(点Cについて\( x \)軸に関して対称な点)になります。そのため,点Dの座標は,
\[ \textbf{D}(-a, \ -b) \]
と表すことができ,点Bと\( x \)座標の符号(点Cと\( y \)座標の符号)を変えた座標で,点Aとは,\( x \)座標,\( y \)座標ともに符号を変えた座標になります。
MOVIE
動画解説
