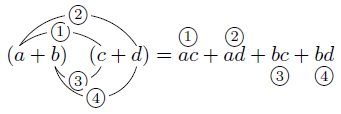次の式を展開し，ア～オに当てはまる数を半角英数字で入力しなさい。

1. $(2x+1)(x+3)=\boxed{\text{ア}}{x}^2+\boxed{\text{イ}}x+\boxed{\text{ウ}}$
2. $(3x+5y)(2x-3y)=\boxed{\text{エ}}{x}^2+xy-\boxed{\text{オ}}{y}^2$

積の形で書かれた式を計算して単項式の和の形に書き表すこと（1つの多項式で表すこと）を，もとの式を展開するといいます。つまり，「かっこをはずしてバラバラにする」ことです。また，積の記号「$\times$」は，

$$x\times y⟶x\cdot y$$

のように，記号「$\cdot$」を用いて省略して表すこともあります。

$(a+b)(c+d)$のような「$\mathbf{\text{（多項式）}}\times \mathbf{\text{（多項式）}}$」を展開するには，主に次のような2つの方法があります。

1. まとまりを1つのものと考える
2. かっこの中に含まれるすべての項を分配する

そこで，この2つの展開の方法で$(a+b)(c+d)$を展開してみます。

1. 「$a+b$」または「$c+d$」をひとまとまりにして展開する。
1. $a+b=A$とすると，
   $$(a+b)(c+d)=A\times (c+d)$$
   という形に変形でき，こうすることで「$\mathbf{\text{（単項式）}}\times \mathbf{\text{（多項式）}}$」の形になります。そこで，分配法則を利用して，
   $$A\times (c+d)=A\times c+A\times d$$
   となります。ここで，$A$を元に戻してあげると，
   $$A\times c+A\times d=(a+b)\times c+(a+b)\times d$$
   となり，さらに「$\mathbf{\text{（多項式）}}\times \mathbf{\text{（単項式）}}$」という形が出てくるので，再度分配法則を用いて，
   $$\begin{array}{rl}(a+b)\times c+(a+b)\times d& =a\times c+b\times c+a\times d+b\times d\\ & =ac+bc+ad+bd\end{array}$$
   となります。
2. $c+d=B$とすると，
   $$(a+b)(c+d)=(a+b)\times B$$
   という形に変形でき，こうすることで「$\mathbf{\text{（多項式）}}\times \mathbf{\text{（単項式）}}$」の形になります。よって，分配法則を利用して，
   $$(a+b)\times B=a\times B+b\times B$$
   となります。ここで，$B$を元に戻してあげると，
   $$a\times B+b\times B=a\times (c+d)+b\times (c+d)$$
   となり，「$\mathbf{\text{（単項式）}}\times \mathbf{\text{（多項式）}}$」という形が出てくるので，再度分配法則を用いて，
   $$\begin{array}{rl}a\times (c+d)+b\times (c+d)& =a\times c+a\times d+b\times c+b\times d\\ & =ac+ad+bc+bd\end{array}$$
   となります。
2. 1の結果から，結局
   
   のように，多項式の各項を順に分配して積を作り，その和を考えればよいことになります。これは，$(a+b)\times (c+d)$を
   $$\mathbf{\text{たての長さ：}}a+b,\mathbf{\text{横の長さ：}}c+d$$
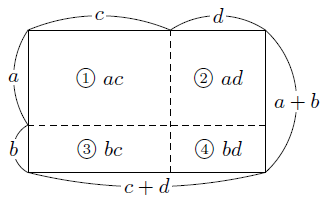
   である長方形の面積であると考えて，次の図のように長方形を4つに分割し，それぞれの長方形の面積の和が全体の面積になることから，
   $$(a+b)(c+d)=ac+ad+bc+bd$$
   になるのだと考えると，イメージがしやすいと思います。

展開した計算結果は，降べきの順で整理するよう心がけてください。