正多面体について次の表を完成させるとき，ア～オに当てはまる図形を選択肢から選び記号を，カ～ノに当てはまる数を半角英数字で入力しなさい。

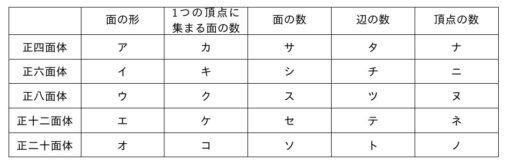
$$\begin{array}{rlrlrl}& a\mathrm{正}\mathrm{三}\mathrm{角}\mathrm{形}& & b\mathrm{二}\mathrm{等}\mathrm{辺}\mathrm{三}\mathrm{角}\mathrm{形}& & c\mathrm{正}\mathrm{方}\mathrm{形}\\ & d\mathrm{直}\mathrm{角}\mathrm{三}\mathrm{角}\mathrm{形}& & e\mathrm{ひ}\mathrm{し}\mathrm{形}& & f\mathrm{正}\mathrm{五}\mathrm{角}\mathrm{形}\end{array}$$

平面だけで囲まれた立体を多面体といいます。普通，立体を作るためには「1つ」の平面だけでなく「多」くの平面が必要であるので，そのような名前になっていると思ってください。

そして，多面体のうち，へこみのない多面体を凸多面体といいます。凸多面体の頂点の数を$v$，辺の数を$e$，面の数を$f$とすると，

$$\begin{array}{rl}\text{（頂点の数）}-\text{（辺の数）}+\text{（面の数）}& =2\\ v-e+f& =2\end{array}$$

という関係が成り立ち，これをオイラーの多面体定理といいます。

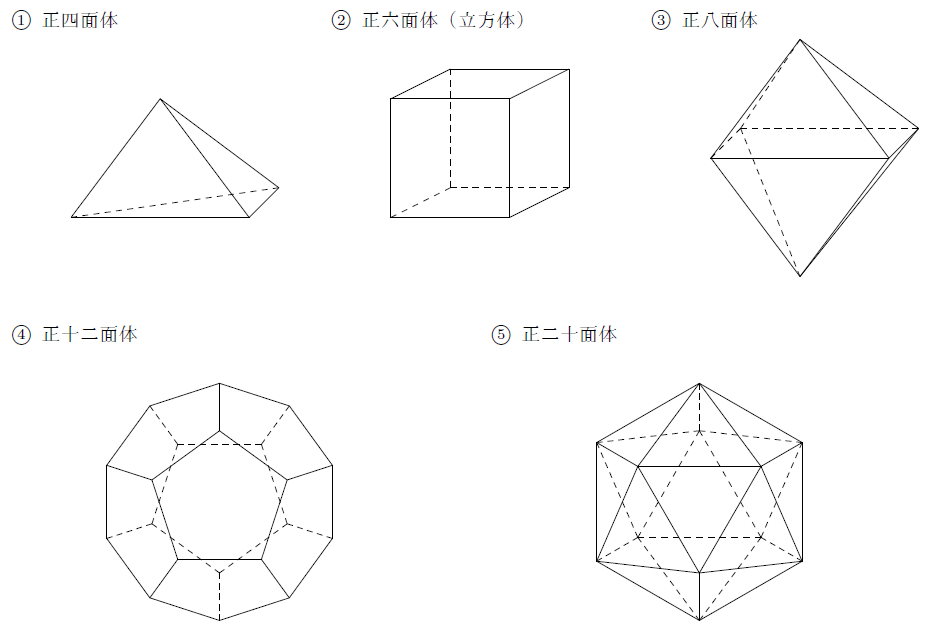
また，合同な多角形で囲まれ，頂点に集まる面の数が等しい多面体を正多面体といい，正多面体は次の5種類だけ存在します。