2014年愛知県A第2問(3)改
- 正解率:100.00%
- 解答数:1
EXERCISE
演習問題
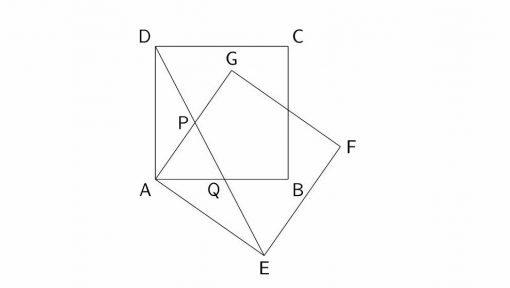
図で,正方形AEFGは,正方形ABCDを,頂点Aを回転の中心として,時計の針の回転と同じ向きに回転移動したものです。また,P,Qはそれぞれ線分DEと辺AG,ABとの交点です。
このとき,
(証明)
①から,
また,
より,
①,②,③から,
よって,
- 1組の辺とその両端の角が,それぞれ等しい
- 2組の辺とその間の角が,それぞれ等しい
- 2組の角が,それぞれ等しい
図で,正方形AEFGは,正方形ABCDを,頂点Aを回転の中心として,時計の針の回転と同じ向きに回転移動したものです。また,P,Qはそれぞれ線分DEと辺AG,ABとの交点です。
このとき,

(証明)
①から,
また,
より,
①,②,③から,
よって,