【解説】
次の図のように点Pが円Oの外部にあり,点Pを通る2直線の一方が円Oと2点A,Bで交わり,もう一方が点Tで接するような場合では,2組の角がそれぞれ等しいので,△PAT∽△PTBとなります。
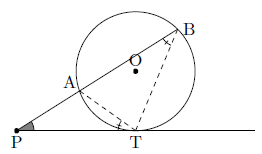
このとき,相似な図形の対応する辺の長さの比は等しいので,
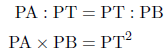
という関係が成り立ち,これも方べきの定理といいます。
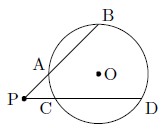
これは,点Pが円Oの外部にあって円と2直線が4つの交点を持つ場合において,点Cと点Dが重なって点Tになったとすると,
PA×PB=PC×PD → PA×PB=PT×PT
となり,どちらも同じ方べきの定理であると考えることができます。
【例題】

【無料動画講義(理論)】
【演習問題】

