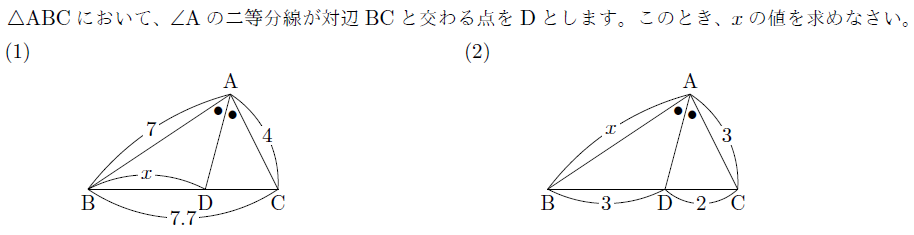
【解説】
次の図のように,△ABCの∠Aの二等分線と対辺BCとの交点をPとします。
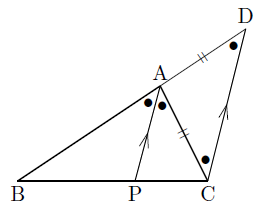
また,頂点Cを通り,APに平行な直線を引き,BAの延長との交点をDとすると,平行線の同位角,錯角は等しくなるので,
∠ADC=∠BAP(同位角),∠ACD=∠CAP(錯角)
となります。
すると,△ACDは,∠ACD=∠ADCより二等辺三角形になるので,
AC=AD……①
となります。
また,AP//DCより,平行線と線分の比の関係から
BP:PC=BA:AD……②
となり,①,②より,
AB:AC=BP:PC
という関係が導き出され,角の2等分線と対辺の交点は,その角をはさむ2辺の比に対辺を分割した点になります。
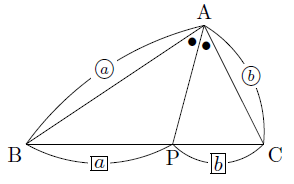
【例題】
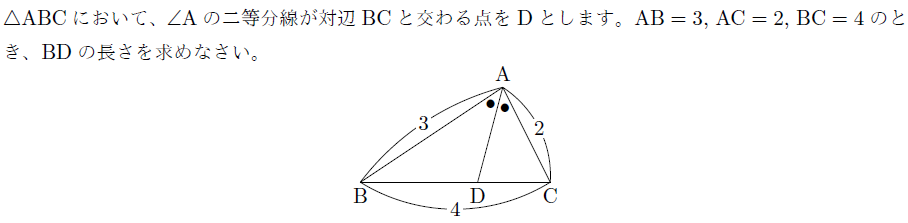
【無料動画講義(理論)】
【演習問題】