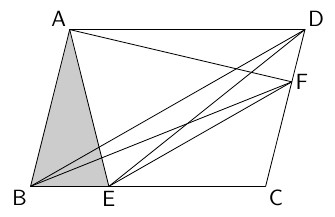
次の図で，$\text{AB} // \text{DC}$，$\text{AD} // \text{BC}$，$\text{EF} // \text{BD}$であるとき，△ABEと面積の等しい三角形を下から3つ選び，ア～ウに当てはまる数を半角英数字で小さい順に入力しなさい。

\begin{align}
&1 \ \triangle{\text{ABD}} & &2 \ \triangle{\text{ABF}} & &3 \ \triangle{\text{AED}} \\
&4 \ \triangle{\text{AEF}} & &5 \ \triangle{\text{DAF}} & &6 \ \triangle{\text{DBE}} \\
&7 \ \triangle{\text{DBF}} & &8 \ \triangle{\text{DEF}} & &9 \ \triangle{\text{FEC}}
\end{align}

次の図のように，直線$l$と直線$m$があり，$l // m$であるとします。

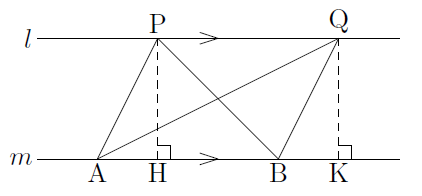
このとき，直線$l$上に2点P，Q，直線$m$上に2点A，Bをとり，△PABと△QABを作ります。さらに，P，Qから直線$m$に垂線を下ろし，直線$m$との交点をH，Kとすると，△PABと△QABの面積はそれぞれ，

\begin{align}
\triangle{\text{PAB}} &=\frac{1}{2} \times (\text{底辺}) \times (\text{高さ}) =\frac{1}{2} \times \text{AB} \times \text{PH} \cdots \cdots ① \\
\triangle{\text{QAB}} &=\frac{1}{2} \times (\text{底辺}) \times (\text{高さ}) =\frac{1}{2} \times \text{AB} \times \text{QK} \cdots \cdots ②
\end{align}

となります。また，$l // m$であるので，2つの直線の距離は等しくなり，

\[ \text{PH} =\text{QK} \cdots \cdots ③ \]

①～③より，

\begin{align}
\frac{1}{2} \times \text{AB} \times \text{PH} &=\frac{1}{2} \times \text{AB} \times \text{QK} \\
\triangle{\text{PAB}} &=\triangle{\text{QAB}}
\end{align}

となることがわかります。

このように，$\text{PQ} // \text{AB}$ならば，△PABと△QABの底辺と高さが等しくなるので，2つの三角形の面積も等しくなります。