【解説】
ある物体が直線上を一定の加速度で運動するとき,これを等加速度直線運動といいます。
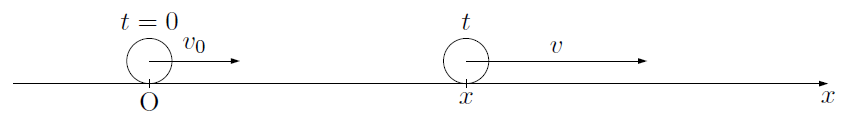
ここで,$x$軸上を一定の加速度$a$,時刻$t=0$に原点Oを初速度(時刻$t=0$における物体の速度)$v_0$で運動(等加速度直線運動)する物体を考えます。
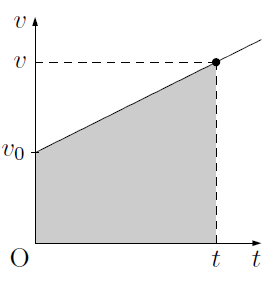
このときの等加速度直線運動を$v-t$グラフで表すと,加速度が一定であるので,上の図のような傾きが一定の直線になります。この直線は,傾きが加速度$a$,切片が初速度$v_0$ であるので,時刻$t$における速度を$v$とすると,
$$v =at +v_0 \ \ \ \ (v =v_0 +at)\cdots \cdots ①$$
と表すことができます。加速度は1 [s]あたりの速度の変化量であるので,$t$ [s]間であれば速度の変化量は$at$になります。つまり,速度は初速度$v_0$ から$t$ [s]間で$at$だけ変化するので,①の関係式になるのだと理解できます。
次に,時刻$t$における物体の位置を$x$とすると,位置$x$は$v-t$グラフと$t$軸とで囲まれた部分の面積(図の影を付けた台形の面積)になるので,
$$\begin{align}x &=\frac{1}{2}(v_0 +v)t =\frac{1}{2}t\{ v_0 +(v_0 +at)\} \\&=\frac{1}{2}t(2v_0 +at) \\&=v_0 t +\frac{1}{2}at^2 \cdots \cdots ②\end{align}$$
と表すことができます。
また,①の式は$\displaystyle t =\frac{(v -v_0)}{a}$と変形できるので,これを②式に代入すると,
$$\begin{align} x &=v_0 +\frac{1}{2}at^2 =\frac{1}{2}t(2v_0 +at) \\&=\frac{1}{2} \frac{v -v_0}{a}\left( 2v_0 +a\frac{v -v_0}{a} \right) \\ 2ax &=(v -v_0)(v +v_0) \\ &=v^2 -{v_0}^2 \cdots \cdots ③ \end{align}$$
という関係を導き出すことができ,等加速度直線運動では①,②,③の式を利用して,位置,速度,加速度を求めることができます。
【例題】

【解説動画講義(理論)】
【解説動画講義(シミュレーション)】
【演習問題】

