相対速度（平面上の運動）

【解説】

平面上を運動するときにおいても，「速度」と言われれば地面に対する速度を一般的に考えますが，動いている2つの物体A，Bがあるとき，Aから見たBの速度（加速度）を考えることもあり，そのことをAに対するBの相対速度（加速度）といいます。

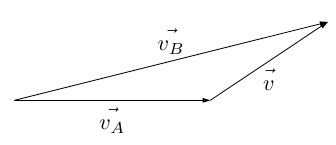
ここで，Aの速度を $\vec{v_{A}}$ ，Bの速度を $\vec{v_{B}}$ ，Aに対するBの相対速度を $\vec{v}$ とします。Aの速度に，Aから見たBの速度（Aに対するBの相対速度）を合成するとBの速度になるので，次のように表すことができます。

$\vec{v_{A}} + \vec{v} = \vec{v_{B}}$

このことから，Aに対するBの相対速度 $\vec{v}$ は，

$\vec{v} = \vec{v_{B}} - \vec{v_{A}}$

で求めることができます。（相対加速度においても同様です。）

このとき，相対速度（加速度）も「向き」と「大きさ」を併せ持った量（ベクトル量）であるので，ベクトルを用いて図示すると，始点をそろえて2つの速度（ベクトル）を表したとき，基準となる速度（ベクトル）の終点から，他方の速度（ベクトル）の終点を結ぶベクトルが相対速度を表すベクトルになります。