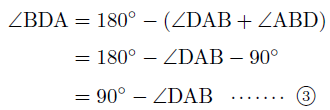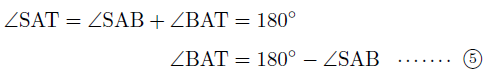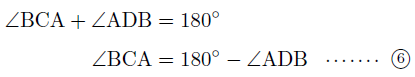【解説】
次の図のような円に内接する四角形APBCを考えます。(直線ATは点Aにおける円の接線)
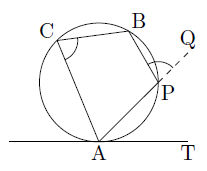
このとき,円に内接する四角形の性質から,1つの外角の大きさは,それと隣り合う内角の対角の大きさに等しいので,
∠BCA=∠BPQ
となります。
ここで,A,B,Cを固定したままPを円周上に沿ってAに近づけていくと,∠BPQと∠BATは一致します。
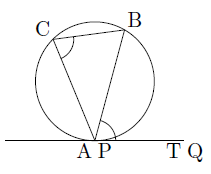
このことから,
∠BCA=∠BAT(=∠BPQ)
となることが予想されます。実際に,「円の接線とその接点を通る弦のつくる角は,その角の内部にある弧に対する円周角に等しい」ということが成り立ち,これを接弦定理といいます。
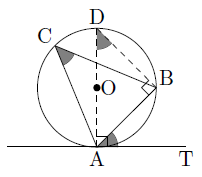
- ∠BATが鋭角であるとき

直径ADを引くと,∠BDA,∠BCAは に対する円周角であるので,
に対する円周角であるので,
∠BDA=∠BCA……①
円の中心と接点を結んだ直線は,接線と垂直に交わるので∠DAT=90°。このことから,
∠BAT=∠DAT-∠DAB=90°-∠DAB……②
また,ADは円Oの直径であるので,半円の弧に対する円周角∠ABD=90°。よって,△DABの内角の和は180°になることから,

①~③より,∠BCA=∠BAT - ∠BATが直角(∠BAT=90°)のとき

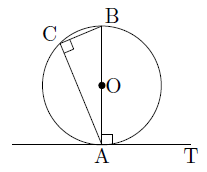
ABは円Oの直径であるので,半円の弧に対する円周角は90°になることから,∠BCA=90°。よって,
∠BCA=∠BAT - ∠BATが鈍角であるとき

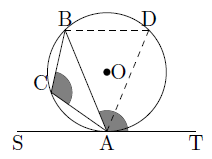
図のように,線分ABに対しCと反対側の円周上に点Dをとります。∠BATが鈍角のとき,∠SABは鋭角であるので,1より,
∠SAB=∠ADB……④
一直線の作る角は180°であるので,

また,円に内接する四角形の向かい合う内角の和は180°であるので,

④~⑥より,
∠BCA=∠BAT
【例題】

【無料動画講義(理論)】
【演習問題】