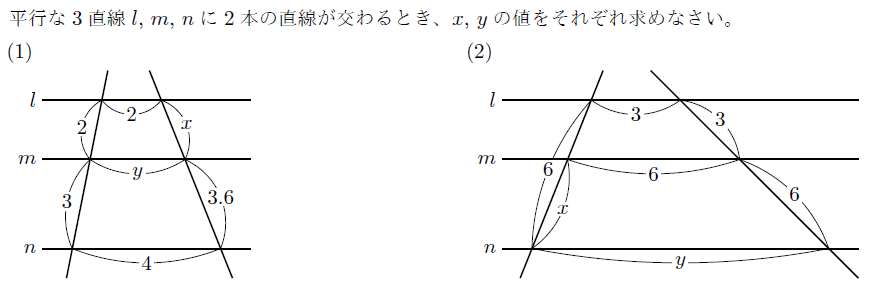
【解説】
次の図のように,△ABCの2辺AB,AC上に,PQ//BCとなるように2点P,Qをとります。
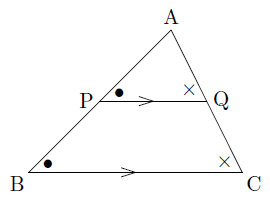
このとき,△APQと△ABCで,PQ//BCより,同位角は等しいので,
∠APQ=∠ABC……①
∠PQA=∠BCA……②
①,②より,2組の角がそれぞれ等しいので,
△APQ∽△ABC
相似な図形の対応する辺の比は等しいので,
AP:AB=AQ:AC=PQ:BC
となります。
このとき,次の図のように,
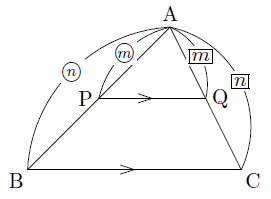
AP:AB=AQ:AC=m:n
とすると,
AP:PB=m:(n-m),AQ:QC=m:(n-m)
となるので,
AP:PB=AQ:QC
という関係が成り立ちます。
ここで,次の図のように,平行な3直線l,m,nに2本の直線が交わり,その交点をそれぞれA,B,C,D,E,Fとします。
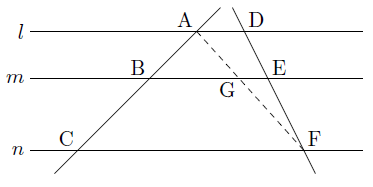
さらに,点Aと点Fを結び,AFと直線mとの交点をGとすると,m//nより,
AB:BC=AG:GF……③
同様にして,l//mより,
AG:GF=DE:EF……④
よって,③,④より,
AB:BC=DE:EF
という関係が成り立ち,以上のことから,平行線によって分割された線分の比は等しくなります。
【例題】
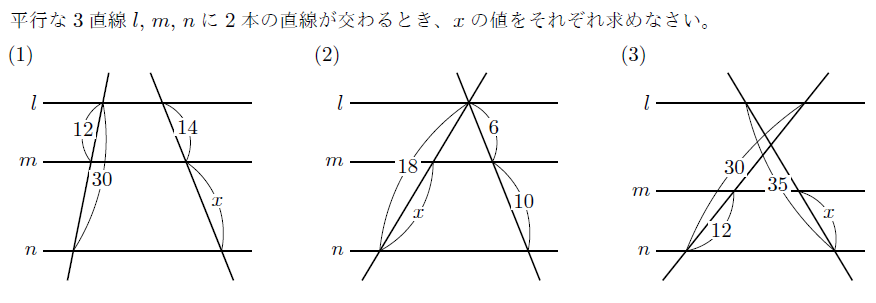
【無料動画講義(理論)】
【演習問題】