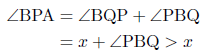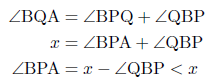【解説】
3つの点を取る円は必ずかくことができますが,4つ以上の点を通る円は必ずかくことができるわけではありません。そこで,ここでは4つの点が同一円周上にある条件(共円条件)について考えます。
次の図のように,円Oの周上に3点A,B,Cをとります。
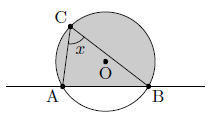
図の色付きの図形のように,円の弧と弦とで囲まれた図形を弓形といい,弧ABと弧上の点Cを用いて,「弓形ACB」といいます。
ここで,弧ABに対する円周角∠BCAの大きさをxとし,直線ABに対してCと同じ側に点Pをとりますが,点Pのとり方には,次の3つの場合が考えられます。
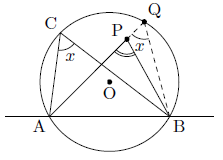
- 点Pが弓形ACBの内部にある場合

APの延長と円との交点をQとすると,∠BQAは に対する円周角であるので,円周角の定理から,
に対する円周角であるので,円周角の定理から,
∠BQA=∠BCA=x
∠BPAは,△QPBに着目すると∠QPBの外角になるので,

となり, に対する円周角よりも大きくなります。
に対する円周角よりも大きくなります。 - 点Pが弓形ACBの弧上にある場合

∠APBは に対する円周角であるので,円周角の定理から,
に対する円周角であるので,円周角の定理から,
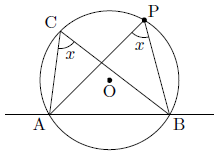
∠BPA=∠BCA=x - 点Pが弓形ACBの外部にある場合

APと円との交点をQとすると,∠BQAは に対する円周角であるので,円周角の定理から,
に対する円周角であるので,円周角の定理から,
∠BQA=∠BCA=x
∠BQAは,△PQBに着目すると∠PQBの外角になるので,

となり,∠APBは に対する円周角よりも小さくなります。
に対する円周角よりも小さくなります。
以上のことをまとめると,
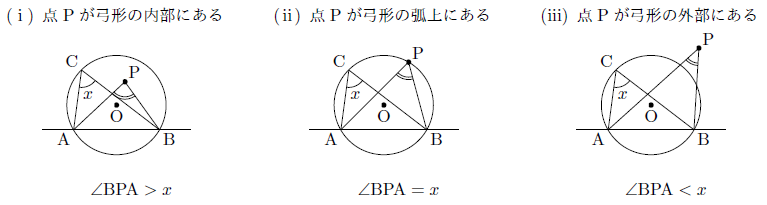
という関係があることになります。
このことから,4点A,B,C,Pについて,点C,Pが直線ABに対して同じ側にあり,
∠BPA=∠BCA
ならば,点Pは3点A,B,Cを通る円(円O)の円周上に存在する(円の内部や外部には存在しない)ので,4点A,B,C,Pは同一円周上にあることになり,円周角の定理の逆が成り立つことがわかります。