【解説】
2つの三角形が合同になるための条件は,
- 3辺がそれぞれ等しい
- 2辺とその間の角がそれぞれ等しい
- 1辺とその両端の角がそれぞれ等しい
という3つの場合がありました。合同な図形は,
- 対応する線分の長さ
- 対応する角の大きさ
がそれぞれ等しくなりますが,相似な図形では,
- 対応する線分の長さの比
- 対応する角の大きさ
がそれぞれ等しくなります。このことから,合同な図形と相似な図形では,
「対応する線分の長さ」と「対応する線分の長さの比」
という部分が異なるので,三角形の合同条件の部分を
「対応する線分の長さ」→「対応する線分の長さの比」
という意味になるように変えることで,三角形の合同条件を三角形の相似条件に変えることができます。つまり,三角形の相似条件は,
- 3辺がそれぞれ等しい→3組の辺の比がすべて等しい
- 2辺とその間の角がそれぞれ等しい→2組の辺の比とその間の角がそれぞれ等しい
- 1辺とその両端の角がそれぞれ等しい→2組の角がそれぞれ等しい
となります。3の条件は,「1組の辺の比とその両端の角がそれぞれ等しい」としたくなりますが,△ABC∽△DEFであるとき,
AB:DE=BC:EF
のように2組の辺の比が等しいことは示せますが,1組の辺の比は
AB:DE
のようになってしまうので,「1組の辺の比が等しい」という言葉は,意味のわからないものになってしまいます。そのため,その部分の言葉は除く必要があるので注意してください。
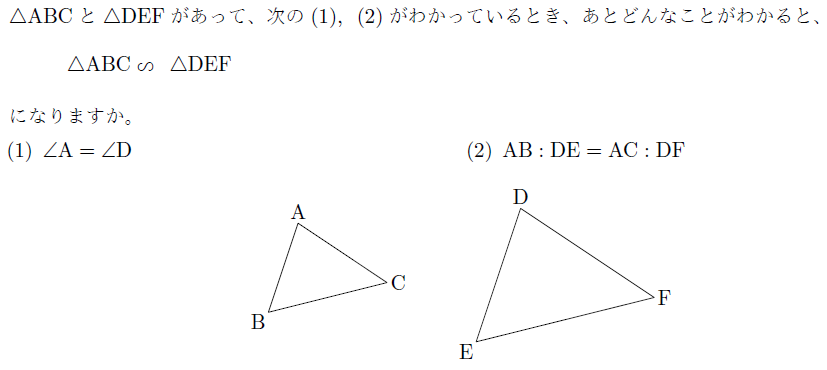
【例題】