次の図の中から2直線の位置関係が次のようになっているものをそれぞれ記号で答えるとき，ア～カに当てはまる数を半角英数字で入力しなさい。ただし，数は小さい順に入力すること。

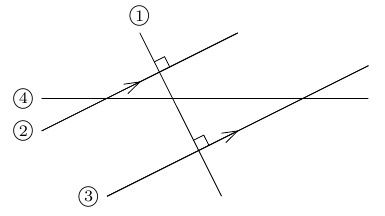
1. 平行：直線\( \fbox{ア} \)と直線\( \fbox{イ} \)
2. 垂直：直線\( \fbox{ウ} \)と直線\( \fbox{エ} \)，直線\( \fbox{オ} \)と直線\( \fbox{カ} \)

2つの直線に関する位置の関係について考えるとき，手元に2つの棒状のもの（ペンなど）を用意し，それらを動かしていろいろな置き方をしてみると，イメージがつかみやすくなります。

同じ平面上に2つの直線\( l \)，\( m \)があるとき，この2直線の位置関係には，次の3つの場合が考えられます。

①のように2つの直線が1点で交わるとき，その交点をPとします。このとき，∠Pの大きさが90度（直角）であると，\( l \)と\( m \)は垂直である（直交する）といい，\( l \perp m \)と表します。また，図では次の図のようにして直角であることを表します。

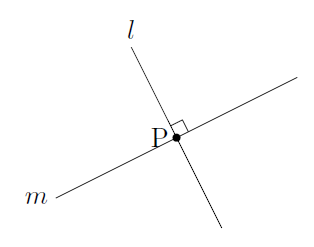
垂直な2直線の一方を，他方の垂線といいます。

次の図のように点Pから直線\( l \)上の点Qと結んだとき，\( \text{PQ} \perp l \)となると線分PQの長さは最も短くなり，この長さを点Pと直線\( l \)との距離といいます。2点A，B間の距離が線分ABの長さになりますが，これも，2点A，Bを結んだときに「最も短くなる」長さだからです。

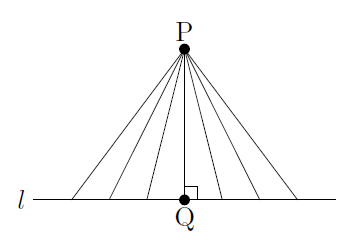
このように，数学で「距離」を考えるときは，「最短の長さ」になります。

次に，②のように2つの直線が交わらないとき，\( l \)と\( m \)は平行であるといい，\( l // m \)と表します。また，図では次の図のようにして，平行である2つの直線に同じ向きの矢印をつけることで，平行であることを表します。

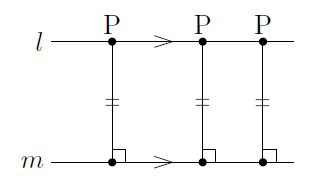
このとき，直線\( l \)上に点Pをとったとき，点Pが直線\( l \)上のどこにあっても，点Pと直線\( l \)との距離は一定になり，この距離を平行な2直線\( l \)，\( m \)間の距離といいます。