【講義】有効数字の表し方
- 正解率:12.35%
- 解答数:81
EXAMPLE
例題
次の近似値を,かっこ内に示された数が有効数字のけた数として,整数部分が1けたの小数と10の累乗または,その逆数との積の形で表すとき,ア~オに当てはまる数を半角英数字で入力しなさい。
- \( 37 \quad [2] \longrightarrow \fbox{ア} \times 10 \)
- \(\displaystyle 0.043 \quad [2] \longrightarrow \fbox{イ} \times \frac{1}{10^{\fbox{ウ}}} \)
- \( 618000 \quad [4] \longrightarrow \fbox{エ} \times 10^{\fbox{オ}} \)
TEXT
テキスト解説
重さを量ったところ,測定値が次のようになった2つのおもりがあるとします。
- \( 3.8 \)kg
- \( 3.80 \)kg
どちらも同じおもりのように感じますが,測定値は近似値の1つなので,それぞれ端数の部分を四捨五入して得られた値です。つまり,それぞれのおもりの真の値の範囲は次のようになっていて,その値を四捨五入することで得られたものになります。
- \( 3.8 \)kg:\( 3.75 \leqq \text{(真の値)} <3.85 \)
- \( 3.80 \)kg:\( 3.795 \leqq \text{(真の値)} <3.805 \)
このように,同じように表された数値でも,その数値の持つ意味は異なり,測定値などの近似値において信頼のできる数字のことを,有効数字といいます。このとき,(1)の「3.8kg」は「有効数字2けた」,(2)の「3.80kg」は「有効数字3けた」の近似値になります。
しかし,測定値が「200g」のような表記では,
- 有効数字1けたのとき:\( 150 \leqq \text{(真の値)} <250 \)
- 有効数字2けたのとき:\( 195 \leqq \text{(真の値)} <205 \)
- 有効数字3けたのとき:\( 199.5 \leqq \text{(真の値)} <200.5 \)
のような場合が考えられ,どこまで測定してどこを四捨五入した値なのか判断できないので,有効数字が何けたなのかわかりません。そこで,有効数字をはっきりさせるために,次のように整数部分が1けたの小数と,10の累乗,または10の累乗の逆数との積の形に表すことが多くあります。
- 有効数字1けたのとき:\( 2 \times 10^2 \)
- 有効数字2けたのとき:\( 2.0 \times 10^2 \)
- 有効数字3けたのとき:\( 2.00 \times 10^2 \)
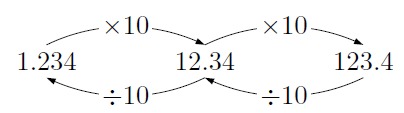
小数の掛け算や割り算では,「\( \times 10 \)」すると小数点は右に,「\( \div 10 \)」すると小数点は左に1つ動きます。
そこで,近似値を有効数字がよくわかる書き方にするために,次の手順で行います。
- 目的の数だけ有効数字をぬき出す。
- ぬき出した数を整数部分が1けたの小数にする。
- 元の数と同じになるように10の累乗,または10の累乗の逆数を掛ける。
MOVIE
動画解説
