2元1次方程式のグラフ

【解説】

2元1次方程式x+y=5を満たすx，yの組は，次のようになります。

x	1	2	3	4	5	6	7	8
y	4	3	2	1	0	-1	-2	-3

このxとyの組(x，y)を座標とする点を図に表してみると次の図のようになり，x，yの組をもっと細かく，

(0.1，4.9)， (0.2，4.8)， (0.3，4.7)，…

のようにして考えていくと，そのxとyの組を座標とする点を図に表したとき，それらの点が集まって，図のような直線に近づきます。

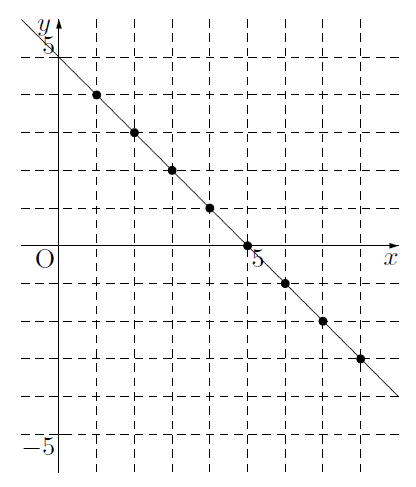
このようにして，2元1次方程式の解となる点(x，y)の全体は，1次関数のグラフと一致し，この直線を方程式のグラフといいます。

p，q，rを定数とするとき，2元1次方程式px+qy=r（ただし，q≠0）をyについて解くと，

と変形でき，-p/q=a，r/q=bとすると，②の式は，y=ax+bと表すことができます。つまり，2元1次方程式をyについて解くと，1次関数y=ax+bの形に変形することができるので，px+qy=r（q≠0）のグラフは直線になります。

このときp=0であるとすると，②の式はy=r/qとなり，xの値にかかわらず常にyの値がr/qであることを表しています。この方程式をグラフにすると，次の図のように点(0，r/q)を通り，x軸に平行な直線になります。

また，p≠0，q=0のとき，①の式は，x=r/pとなり，yの値にかかわらず常にxの値がr/pであることを表しています。この方程式をグラフにすると，上の図のように(r/p，0)を通り，y軸に平行な直線になります。

このことから，x=0という方程式のグラフはy軸，y=0という方程式のグラフはx軸になります。