【講義】角の二等分線
EXAMPLE
例題
下の図において,\( \angle \text{AOB} \)の二等分線を作図しなさい。
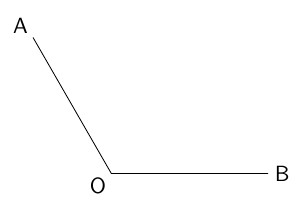
TEXT
テキスト解説
角を2等分する半直線を角の二等分線といいます。
ここでは,次の図のような\( \angle \text{AOB} \)の二等分線を作図します。
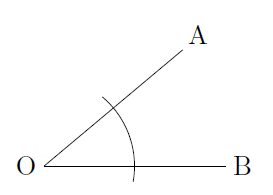
\( \angle \text{AOB} \)の二等分線を作図するには,まず,点Oを中心とする円をかきます(上図)。このとき,辺OAと辺OBとの交点がわかればよいので,円をすべてかく必要はありません。
次に,辺OAと辺OBとの交点(ここではわかりやすいようにP,Qとします)をそれぞれ中心とするような等しい半径の円をかきます(下図)。このとき,円の半径は,2つの円が交わればどのような長さでもかまいませんが,OPと同じ長さにしておくと作図が楽です。また,2つの円の交点がわかればよいので,円をすべてかく必要はありません。
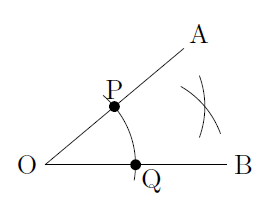
最後に,点Oから2つの円の交点(ここではわかりやすいようにRとします)を通る半直線を引くと,この半直線(半直線OR)が\( \angle \text{AOB} \)の二等分線になります。
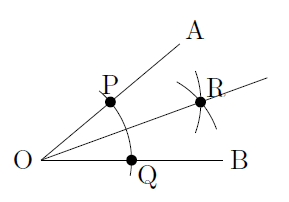
なぜ半直線ORが角の二等分線になるかは,△PORと△QORという2つの三角形が合同になるからです。(三角形の合同を学習してから,下の解説を読んでみてください。)
△PORと△QORにおいて,
\[ \text{PO} =\text{QO},\text{PR} =\text{QR},\text{OR} =\text{OR} \]
と3つの辺が等しいため2つの三角形が合同になります。合同な図形では対応する角の大きさが等しくなるため,
\[ \angle \text{POR} =\angle \text{QOR} \]
となり,半直線ORは\( \angle \text{AOB} \)の二等分線であることがわかります。
このように,角の二等分線は次の手順により作図することができます。
- 角の頂点を中心とする円をかく
- その円と角を作る2辺との交点を中心とするような等しい半径の円をかく
- 角の頂点から,2つの円の交点を通る半直線を引く
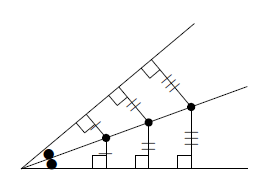
また,角の二等分線上の点は,次の図のように2辺から等しい距離にある点の集まりになります。
MOVIE
動画解説
