次の半球の表面積と体積を求め，ア，イに当てはまる数を半角英数字で入力しなさい。

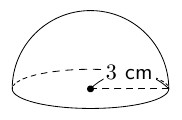
1. 表面積：\( \fbox{ア} \ \pi \ \text{cm}^2 \)
2. 体積：\( \fbox{イ} \ \pi \ \text{cm}^3 \)

次の図のような，中心O，半径rの球を考えます。

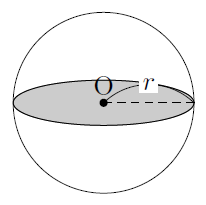
球の表面積は，球の中心Oを通る面で切ったときにできる半径\( r \)の円（図の色のついた部分）の4倍であることが知られています。つまり，球の表面積を\( S \)とすると，次の式で表されます。

\[ S =\pi r^2 \times 4 =4 \pi r^2 \]

次に，半径\( r \)の球を，次の図のような角錐でものすごく細かく分割していきます。

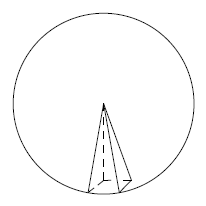
分割した角錐の体積の和が球の体積になりますが，1つ1つの角錐の体積は，

\[ \text{（角錐の体積）} =\frac{1}{3} \times \text{（底面積）} \times \text{（高さ）} \]

で求めることができ，角錐の高さはすべて\( r \)になります。また，角錐の底面をすべて合わせると球の表面になるので，

\[ \text{（角錐の底面積の和）} =\text{（球の表面積）} \]

という関係になっています。このことから，球の体積を\( V \)とすると，次のような式で表すことができます。

\begin{align}
V &=\text{（角錐の体積の和）} \\
&=\frac{1}{3} \times \text{（底面積の和）} \times \text{（高さ）} \\
&=\frac{1}{3} \times \text{（球の表面積）} \times r \\
&=\frac{1}{3} \times 4\pi r^2 \times r \\
&=\frac{4}{3}\pi r^3
\end{align}