【講義】特別な多角形の内角の和
- 正解率:22.22%
- 解答数:27
EXAMPLE
例題
次の角の大きさを求め,ア,イに当てはまる数を半角英数字で入力しなさい。

- $\angle{x} =\fbox{ア}^{\circ}$
- (黒くぬった角度の和)$=\fbox{イ}^{\circ}$
TEXT
テキスト解説
次の図のような図形(ここでは,「ブーメラン型」と呼ぶことにします。)において,$\angle{x}$の大きさを考えます。
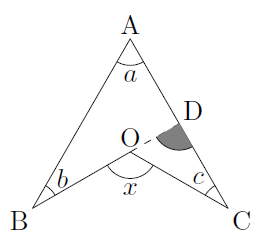
図のように,BOの延長とACとの交点をDとすると,△ABDにおいて外角の定理を利用することで,
\[ \angle{\text{BDC}} =\angle{a} +\angle{b} \cdots \cdots ① \]
さらに,△OCDにおいても外角の定理を利用すると,①より,
\begin{align}
\angle{x} &=\angle{\text{BDC}} +\angle{c} \\
&=\angle{a} +\angle{b} +\angle{c}
\end{align}
という関係が導き出されます。
また,次の図のような図形(ここでは,「五芒星 (ごぼうせい) 型」と呼ぶことにします。)において,内角の和($\angle{a} +\angle{b} +\angle{c} +\angle{d} +\angle{e}$)について考えます。
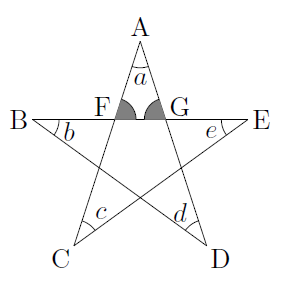
図のように,AC,ADとBEとの交点をそれぞれF,Gとします。△FCE,△BDGに着目して,それぞれに外角の定理を利用すると,
\[ \angle{\text{AFG}} =\angle{c} +\angle{e}, \quad \angle{\text{FGA}} =\angle{b} +\angle{d} \]
このとき,△AFGに着目すると,三角形の内角の和は$180^{\circ}$であるので,
\begin{align}
\angle{\text{A}} +\angle{\text{AFG}} +\angle{\text{FGA}} &=180^{\circ} \\
\angle{a} +(\angle{c} +\angle{e}) +(\angle{b} +\angle{d}) &=180^{\circ} \\
\angle{a} +\angle{b} +\angle{c} +\angle{d} +\angle{e} &=180^{\circ}
\end{align}
となります。
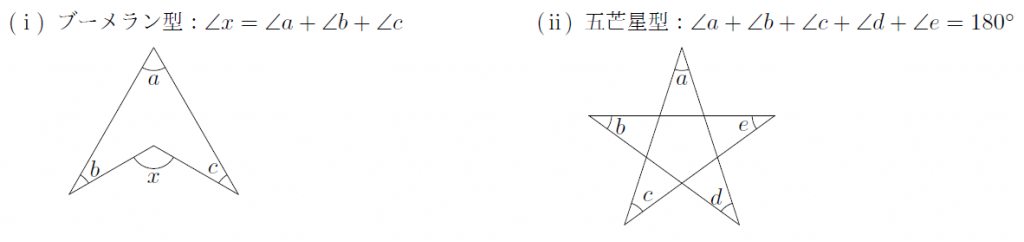
このような内角の大きさの関係は,角度を求める問題でしばしば利用されるので,公式として覚えておくようにしましょう。
MOVIE
動画解説
