【講義】比例のグラフと変域
EXAMPLE
例題
次の関数のグラフをかきなさい。
- \( y =x \ \ \ \ \ (1 \leqq x \leqq 5) \)
- \( y =-2x \ \ \ \ \ (-1 \leqq x \leqq 2) \)
TEXT
テキスト解説
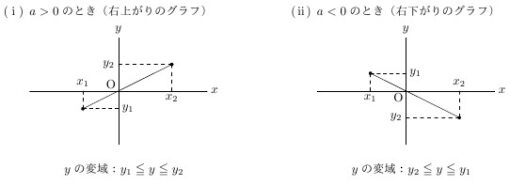
ある関数について,\( x \)の変域から\( y \)の変域を求めたり,その逆に,\( y \)の変域から\( x \)の変域を求めたりするような問題では,関数のグラフをかいたりイメージすることが大切です。このとき,関数のグラフはその変域の部分だけを表し,残りの部分はかかないか点線で表すようにします。
比例\( y =ax \)において,\( x \)の変域が\( x_1 \leqq x \leqq x_2 \)となっているとき,次のように,関数を表す式の横に\( x \)の変域をかっこの中に入れて表されることがあります。
\[ y =ax \ \ \ \ \ (x_1 \leqq x \leqq x_2) \]
また,このときの\( y \)の変域は,比例のグラフが原点を通る直線(線分)になることから,次のようになります。
MOVIE
動画解説
