【講義】多角形の外角の和
- 正解率:66.67%
- 解答数:3
EXAMPLE
例題
次の多角形の1つの内角の大きさを求め,ア,イに当てはまる数を半角英数字で入力しなさい。
- 正八角形
- 正十角形
\[ \text{1つの内角の大きさ:}\fbox{ア}^{\circ} \]
\[ \text{1つの内角の大きさ:}\fbox{イ}^{\circ} \]
TEXT
テキスト解説
ここではまず,次の図のような三角形(△ABC)の外角の和($\angle{a’} +\angle{b’} +\angle{c’}$)について考えてみたいと思います。
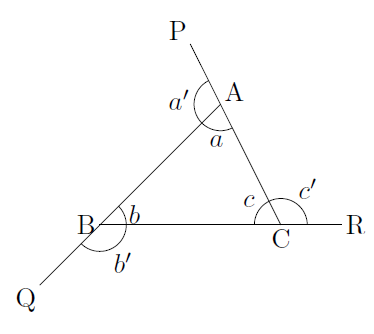
一直線のつくる角は$180^{\circ}$であるので,
\[ \angle{a} +\angle{a’} =\angle{b} +\angle{b’} =\angle{c} +\angle{c’} =180^{\circ} \]
になります。このことから,
\begin{align}
(\angle{a} +\angle{a’}) +(\angle{b} +\angle{b’}) +(\angle{c} +\angle{c’}) &=180^{\circ} \times 3 \\
\angle{a} +\angle{a’} +\angle{b} +\angle{b’} +\angle{c} +\angle{c’} &=540^{\circ} \\
(\angle{a} +\angle{b} +\angle{c}) +(\angle{a’} +\angle{b’} +\angle{c’}) &= 540^{\circ} \cdots \cdots ①
\end{align}
のような関係式を作ることができます。また,三角形の内角の和は$180^{\circ}$なので,
\[ \angle{a} +\angle{b} +\angle{c} =180^{\circ} \cdots \cdots ② \]
です。よって,①,②より,
\begin{align}
(\angle{a} +\angle{b} +\angle{c}) +(\angle{a’} +\angle{b’} +\angle{c’}) &= 540^{\circ} \cdots \cdots ① \\
180^{\circ} +(\angle{a’} +\angle{b’} +\angle{c’}) &=540^{\circ} \\
\angle{a’} +\angle{b’} +\angle{c’} &=540^{\circ} -180^{\circ} \\
&=360^{\circ}
\end{align}
となり,三角形の外角の和($\angle{a’} +\angle{b’} +\angle{c’}$)は$360^{\circ}$であることがわかります。
同じようにして$n$角形の場合も考えてみると,
\[ (\text{1つの内角} +\text{1つの外角}) \text{の和} =180^{\circ} \times n \]
となるので,
\[ (n\text{角形の内角の和})+(n\text{角形の外角の和}) =180^{\circ} \times n \cdots \cdots ③ \]
と表すことができます。また,$n$角形の内角の和は
\begin{align}
(n\text{角形の内角の和}) &=180^{\circ} \times (n -2) \\
&=180^{\circ} \times n -180^{\circ} \times 2 \\
&=180^{\circ} \times n -360^{\circ} \cdots \cdots ④
\end{align}
であるので,③,④より
\begin{align}
(n\text{角形の内角の和})+(n\text{角形の外角の和}) &=180^{\circ} \times n \cdots \cdots ③ \\
(180^{\circ} \times n -360^{\circ}) +(n\text{角形の外角の和}) &=180^{\circ} \times n \\
(n\text{角形の外角の和}) &=180^{\circ} \times n -180^{\circ} \times n +360^{\circ} \\
&=360^{\circ}
\end{align}
となり,多角形の外角の和は,どのような多角形であっても常に$360^{\circ}$になります。と,原理的にはそうなりますが,ちょっと説明が難しいですよね。このようになることをもう少し感覚的に考えてみましょう。
まず,自分が回転いすにすわっていると思ってください。そして,先ほどの図において,頂点Aの位置にいてそこからPの方向に向いています。そこから,$\angle{a’}$だけ回転して頂点B(Q)の方向に向き,頂点Bに向かっていきましょう。頂点Bに着いたらそこで止まり,$\angle{b’}$だけ回転して頂点C(R)の方に向きます。そして,また頂点Cに向かっていき,頂点Cに着いたら止まり,$\angle{c’}$だけ回転してAに向かうというようにして△ABCを1周します。イメージできましたか?
最初はPを向いていますね。そこから$\angle{a’}$,$\angle{b’}$,$\angle{c’}$だけ回転したっらまたPの方向を向きました。つまり,1回転したわけです。1回転は$360^{\circ}$ですよね。このことから,
\[ \angle{a’} +\angle{b’} +\angle{c’} =360^{\circ} \]
になります。このことは,三角形に限ったことではなく,どのような多角形でも1周すれば1回転することになるので,外角の和は$360^{\circ}$になります。
MOVIE
動画解説
