【講義】多角形の内角の和
- 正解率:50.00%
- 解答数:6
EXAMPLE
例題
次の多角形の内角の和を求め,ア,イに当てはまる数を半角英数字で入力しなさい。
- 五角形
- 十二角形
\[ \text{内角の和:}\fbox{ア}^{\circ} \]
\[ \text{内角の和:}\fbox{イ}^{\circ} \]
TEXT
テキスト解説
三角形,四角形,五角形など,いくつかの線分で囲まれた図形を多角形といいます。
対角線は頂点と頂点を結ぶことにより引くことができますが,自分自身と自分の隣の頂点には対角線を引くことができません。つまり,$n$角形の場合,$n$個ある頂点から3個の頂点を除いた分だけ,1つの頂点から対角線を引くことができるので,1つの頂点から引くことのできる$n$角形の対角線の本数は$(n -3)$本ということになります。
次の図のように,1つの頂点(ここでは,頂点A)から対角線を1本引くと,三角形を1つ作ることができます。
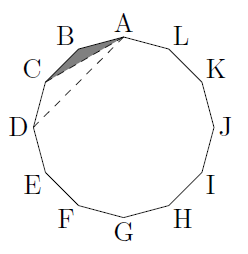
そして,そこから順に対角線を1本ずつ増やすにつれ,できる三角形の個数も1つずつ増えることになります。しかし,最後の1本の対角線を引く場合には,三角形は1つではなく,2つの三角形が作られます。

このことから,多角形を対角線で分割することにより,三角形は対角線の本数よりも1個だけ多く作ることができます。$n$角形の場合,1つの頂点から引くことのできる対角線の本数は$(n -3)$本であったので,対角線によってできる三角形の個数はそれよりも1つ多くなることから,
\[ (n -3) +1 = n -2 \ \text{(個)} \]
となります。そして,「三角形の3つの内角の和は$180^{\circ}$」であることがわかっているので,$n$角形の内角の和は,
\[ (\text{$n$角形の内角の和}) = 180^{\circ} \times (n -2) \]
という式で求めることができます。
MOVIE
動画解説
