垂直二等分線

【解説】

ある線分を垂直に2等分する直線を，垂直二等分線といいます。

ここでは，次の図のような線分ABを垂直に2等分する直線（垂直二等分線）の作図を考えます。

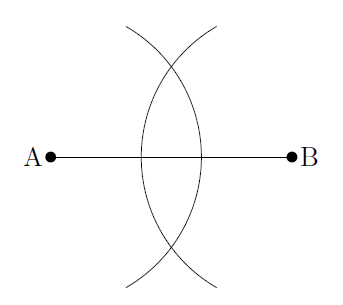
線分ABの垂直二等分線を作図するには，まず，線分の両端の点A，Bをそれぞれ中心とするような等しい半径の円をかきます（上図）。このとき，円の半径は2つの円が交わるような大きさである必要があります。また，2つの円の交点がわかればよいので，円をすべてかく必要はありません。

次に，2つの円の交点（ここではわかりやすいようにP，Qとします）を通る直線を引くと，この直線（直線PQ）が線分ABの垂直二等分線になります。

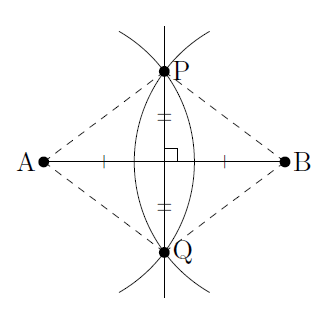
なぜ直線PQが線分ABの垂直二等分線になるかというと，AP，BP，AQ，BQはそれぞれ等しい半径の円の半径であるので，

AP=BP=AQ=BQ

となり，四角形AQBPはひし形になります。ひし形には，

という性質があるので，ひし形AQBPの対角線である線分ABとPQは，PQはABを垂直に2等分する，つまり，ABの垂直二等分線になるからです。

このことから，垂直二等分線は次の手順により作図することができます。

また，線分と垂直二等分線の交点は線分の中点になるので，同じ手順により中点も作図できることになります。

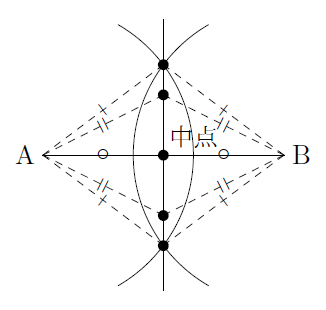
さらに，線分ABの垂直二等分線上の点は，2点A，Bから等しい距離にある点の集まりになります。このことはとても重要なので，しっかり覚えておきましょう。