【講義】円とおうぎ形
TEXT
テキスト解説
次の図のように,平面上のある1点から等しい距離にある点の集まりを円,または,円周といいます。このとき,図のように基準となる点をOとすると,点Oを円の中心といい,Oを中心とする円を円Oと表します。
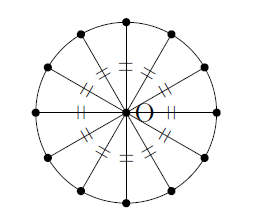
また,次の図のように2点A,Bを両端とする円周の一部を弧ABといいます。2点A,Bにはさまれる弧は,図のように短いもの(劣弧)と長いもの(優弧)の2つがありますが,普通,弧ABというときは短い弧(劣弧)をさします。

そして,円周上の2点を結ぶ線分を弦といい,そのうち,円の中心を通るものを直径といいます。また,円の中心と円周上の点を結ぶ線分を半径といいます。

円の中心を頂点とし,2辺が弧の両端を通る角(∠AOB)を,その弧(弧AB)に対する中心角といいます。また,それとは逆に,弧ABを中心角∠AOBに対する弧といいます。
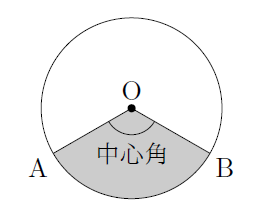
次の図のように1つの弧(弧AB)とその中心角を与える2辺(OA,OB)で囲まれた図形(色のついた部分)をおうぎ形といいます。
MOVIE
動画解説
